前缀和#

定义#

定义很简单，就是一个数列中前n项的和。虽然简单，却是一种非常好用的减少时间复杂度的优化方法。

一维#

原理#

$sum_r=a_1+a_2+......+a_r$

$sum_{l-1}=a_1+a_2+......+a_{l-1}$

$sum_r-sum_{l-1}=a_l+a_l+1+...a_r$

实现#

定义#

1
int sum[N];
2
sum[0]=a[0];
3
for(int i=;i<N;i++){
4
    sum[i]=sum[i-1]+a[i];
5
}

查询#

1
//l到r区间之和
2
cout<<sum[r]-sum[l-1];

二维#

通过图片可知，sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]

不难推出，s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

差分#

差分可以理解为前缀和的逆运算，即如果一个数组a的前缀和数组为b，则数组a是数组b的差分数组。

构造差分#

最简单的构造方法：

1
int a[n],[n];
2
b[0]=a[0];
3
for(int i=1;i<n;i++)
4
{
5
    b[i]=a[i]-a[i-1];
6
}

一维#

一维差分是指给定一个长度为n的序列a，要求支持操作fuc(l,r,c)表示对a[l]~a[r]区间上的每一个值都加上或减去常数c，并求修改后的序列a。

1
//区间[l,r]中的所有值都加上常数c
2
b[l] += c;
3
b[r+1] -= c;
4

5
//上边语句实现原理 b相当于a的辅助数组
6
//把a序列分为[1,l-1],[l,r],[r+1,n]三部分,由差分定义和与前缀和关系可得
7
a[l-1] = b[1]+b[2]+...+b[l-1]; //b[1]~b[l-1]中所有值都未改变，a[l-1]也不变
8
a[l] = b[1]+b[2]+...+b[l-1]+b[l]; //b[1] += c,所以a[l] += c
9
a[l+1] = b[1]+b[2]+...+b[l-1]+b[l]+b[l+1]; //b[1] += c,所以a[l+1] += c
10
... //一直到
11
a[r] = b[1]+b[2]+...b[l]+...+b[r];  //b[1] += c,所以a[l+1] += c
12
a[r+1] = b[1]+b[2]+...b[l]+...+b[r]+b[r+1]; //b[l] += c,b[r+1] -= c;所以a[r+1]不变
13

14
//所以由此可知上面的两个语句（b[l] += c;b[r+1] -= c）可以实现a数组在区间[l,r]内的所有值都加上了常数c

二维#

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。

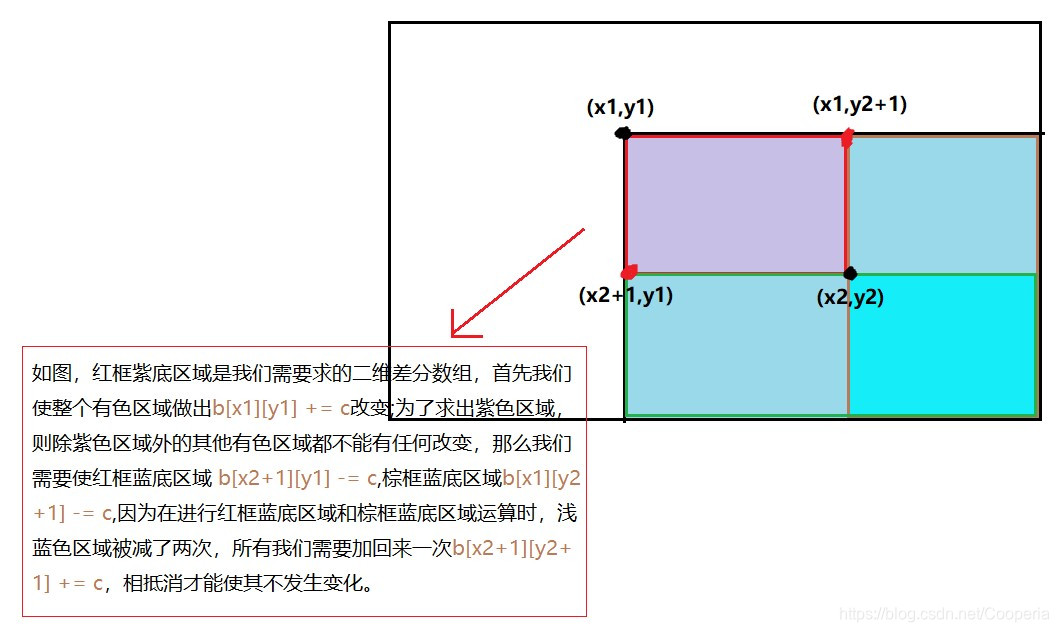
操作#

1
void insert(int x1,int y1,int x2,int y2,int c)
2
{
3
    b[x1][y1] += c;
4
    b[x2+1][y1] -= c;
5
    b[x1][y2+1] -= c;
6
    b[x2+1][y2+1] += c;
7
}

初始化

1
for(int i = 1; i <= n; i++)
2
{
3
    for(int j = 1; j <= m; j++)
4
    {
5
       insert(i,j,i,j,a[i][j]);
6
    }
7
}

区间修改#

对于区间 $[l,r]$ ，所有元素都加上一个值 $c$ ，等价于在差分数组中 $cha_i+=c,cha_{r+1}-=c$ 。然后对这个差分数组求前缀和即可找到答案。

此文章参考了前缀和与差分图文并茂超详细整理（全网最通俗易懂）和算法笔记（六）：差分法的相关内容，在此表示感谢。